Introduction
Dans un monde où le Big Data règne en maître, la capacité à naviguer dans l’océan des données est plus précieuse que jamais. Des graphiques envahissants aux pourcentages qui défilent, la question demeure : comment transformer cette avalanche d’informations en insights significatifs ? La réponse réside dans une compréhension profonde des statistiques, en particulier la distinction entre les statistiques descriptives et inférentielles.
Prenons un exemple concret, inspiré d’une réalité que beaucoup rencontrent lorsqu’ils plongent dans le domaine fascinant de l’analyse de données : imaginez que vous êtes analyste dans un magasin, cherchant à comprendre les dynamiques de prix des articles. Les statistiques descriptives vous serviront de boussole, vous permettant de résumer les données recueillies sur les articles :
- Combien d’articles avez-vous examinés ?
- Quels sont les prix les plus communs et les plus rares ?
- Quelle est la moyenne des prix ?
- Comment les prix varient-ils entre eux ?
Cependant, pour répondre à des questions plus profondes et anticiper des tendances, telles que :
- Les prix moyens diffèrent-ils significativement de ceux d’un autre magasin ?
- Y a-t-il eu une évolution des prix au fil du temps ?
Vous devrez faire appel à la statistique inférentielle. Cette approche vous permet de tirer des conclusions sur l’ensemble de la population des articles du magasin à partir d’un échantillon observé. Elle est cruciale pour effectuer des tests d’hypothèses, calculer des p-valeurs, et estimer des intervalles de confiance.
Ainsi, pour ceux qui se lancent dans le monde de l’analyse de données, maîtriser ces deux facettes des statistiques est essentiel. Les statistiques descriptives et inférentielles offrent un fondement solide non seulement pour comprendre vos données mais aussi pour en déduire des tendances significatives. En construisant sur ces bases, en pratiquant régulièrement, et en restant insatiablement curieux, vous vous équiperez pour naviguer avec succès dans le paysage dynamique et en constante évolution de l’analyse de données.
C’est quoi les statistiques descriptives ?
Les statistiques descriptives s’apparentent à un portrait de vos données. Elles utilisent des indicateurs pour en résumer les caractéristiques essentielles.
Mesures de tendance centrale
Ces mesures permettent de situer le centre de vos données. On retrouve notamment :
La moyenne
Définition: La moyenne est une mesure de tendance centrale qui correspond à la somme de toutes les valeurs d’un ensemble de données divisée par le nombre d’observations.
Formule:
\(\overline{x} = \frac{\sum\limits_{i=1}^{n} x_i}{n}\)
Où :
- \(\overline{x}\) est la moyenne
- \( \sum\limits_{i=1}^{n} x_i\) est la somme de toutes les valeurs de l’ensemble de données
- \({n}\) est le nombre d’observations
Étapes de calcul:
(a) Somme des valeurs:
La première étape consiste à additionner toutes les valeurs de l’ensemble de données.
(b) Division par le nombre d’observations:
Ensuite, on divise la somme obtenue par le nombre d’observations.
(c) Interprétation:
Le résultat obtenu est la moyenne de l’ensemble de données. Elle représente la valeur “centrale” des données.
Exemple:
Considérons l’ensemble de données suivant :
\(A = {12, 15, 10, 14, 18}\)
(a) Somme des valeurs:
\(12 + 15 + 10 + 14 + 18 = 69\)
(b) Division par le nombre d’observations:
\(\frac{69}{5} = 13.8\)

(c) Interprétation:
La moyenne de l’ensemble de données est de 13.8. Cela signifie que, en moyenne, les valeurs de l’ensemble de données sont proches de 13.8.
Le calcul de la moyenne est un processus simple qui consiste à additionner toutes les valeurs d’un ensemble de données et à diviser le résultat par le nombre d’observations. La moyenne est une mesure utile pour résumer un ensemble de données et en comparer plusieurs.
La médiane
Définition: La médiane est une mesure de tendance centrale qui correspond à la valeur qui divise un ensemble de données ordonné en deux groupes de taille égale.
Étapes de calcul:
(a) Tri des données:
La première étape consiste à trier les données par ordre croissant ou décroissant.
(b) Détermination du nombre d’observations:
Ensuite, on détermine le nombre d’observations dans l’ensemble de données.
(c) Calcul de la position de la médiane:
- Si le nombre d’observations est impair, la médiane est la valeur située au milieu du classement.
- Si le nombre d’observations est pair, la médiane est la moyenne des deux valeurs situées au milieu du classement.
(d) Interprétation:
La médiane est la valeur qui sépare les deux moitiés de l’ensemble de données. Elle est utile pour comparer des ensembles de données qui ont des valeurs aberrantes (qu’on nomme outliers dans la langue de Shakespeare, ça sonne cool hein 👌).
Exemple:
Considérons les ensembles de données suivants :
\(A = {14, 18, 7, 10, 9}\) //nombre d’observations impair
\(B = {9, 21, 17, 14, 7, 3, 10, 12}\) //nombre d’observations pair
(a) Tri des données par ordre croissant:
\(A = {7, 9, 10, 14, 18}\)
\(B = {3, 7, 9, 10, 12, 14, 17, 21}\)
(b) Détermination du nombre d’observations:
Pour l’ensemble A
\(n = 5\)
Pour l’ensemble B
\(n = 8\)
(c) Calcul de la position de la médiane:
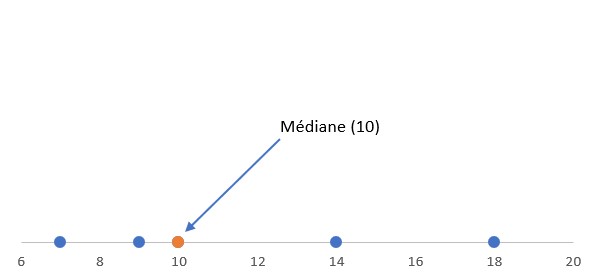
Pour l’ensemble A (nombre d’observation impair), la médiane est la valeur située au milieu du classement, c’est-à-dire la 3ème valeur.
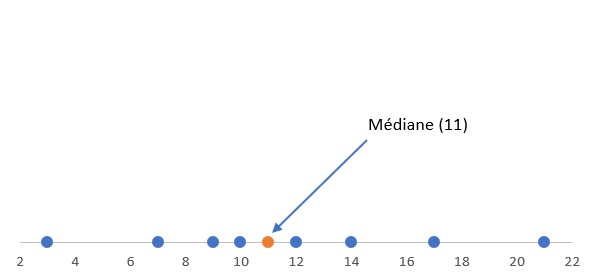
Pour l’ensemble B (nombre d’observation pair), la médiane est la moyenne des valeurs situées en 4ème et 5ème position, c’est-à-dire la moyenne de 10 et 12.
(d) Interprétation:
La médiane de l’ensemble de données A est de 10. Cela signifie que 50% des valeurs sont inférieures à 10 et 50% sont supérieures à 10.
La médiane de l’ensemble de données B est de \(\frac{10 +12}{2}\) , c’est à dire 11.
Le calcul de la médiane est un processus simple qui consiste à trier les données et à déterminer la valeur qui divise l’ensemble de données en deux groupes de taille égale. La médiane est une mesure utile pour comparer des ensembles de données qui ont des valeurs aberrantes (outliers).
Le mode
Définition: Le mode est une mesure de tendance centrale qui correspond à la valeur la plus fréquente dans un ensemble de données.
Étapes de calcul:
(a) Comptage des fréquences:
La première étape consiste à compter le nombre de fois que chaque valeur apparait dans l’ensemble de données.
(b) Identification de la valeur la plus fréquente:
Ensuite, on recherche la valeur qui a la fréquence la plus élevée.
(c) Interprétation:
Le mode est la valeur qui apparait le plus souvent dans l’ensemble de données. Il représente la valeur la plus “typique” des données.
Exemple:
Considérons l’ensemble de données suivant :
\(A = {12, 12, 14, 15, 18, 12}\)
(a) Comptage des fréquences:
| Valeur | Fréquence |
|---|---|
| 12 | 3 |
| 14 | 1 |
| 15 | 1 |
| 18 | 1 |
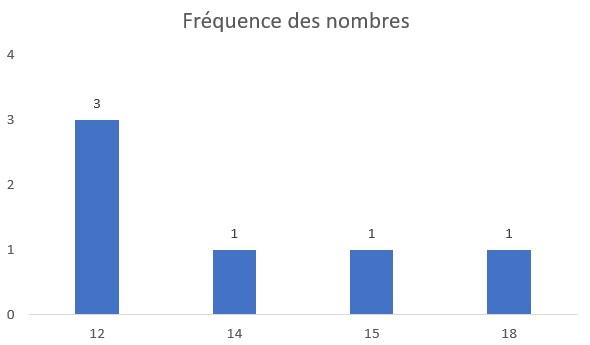
(b) Identification de la valeur la plus fréquente:
La valeur la plus fréquente est 12.
(c) Interprétation:
Le mode de l’ensemble de données est de 12. Cela signifie que la valeur 12 apparait plus souvent que les autres valeurs.
Le calcul du mode est un processus simple qui consiste à compter le nombre de fois que chaque valeur apparait dans un ensemble de données et à identifier la valeur la plus fréquente. Le mode est une mesure utile pour identifier la valeur la plus “typique” d’un ensemble de données.
D’autres mesures aussi importantes dans les statistiques descriptives sont:
Mesures de dispersion
Ces mesures indiquent à quel point vos données sont étalées autour de la mesure de centralisation choisie. On retrouve :
Le minimum, le maximum et la plage (range)
Le minimum d’un ensemble de données est la plus petite valeur qu’il contient.
Le maximum d’un ensemble de données est la plus grande valeur qu’il contient.
Ces deux mesures permettent d’avoir une idée de l’étendue des valeurs dans un ensemble de données. Elles sont faciles à calculer et à comprendre.
La plage est la différence entre le maximum et le minimum d’un ensemble de données. Elle est calculée comme suit :
\({plage} = maximum – minimum\)
La plage est une mesure simple de la dispersion qui ne prend en compte que la différence entre les valeurs maximales et minimales dans un ensemble de données. Elle est utile pour avoir une première idée de la variabilité des données, mais elle ne donne pas d’informations sur la répartition des valeurs entre ces deux bornes.
Exemple:
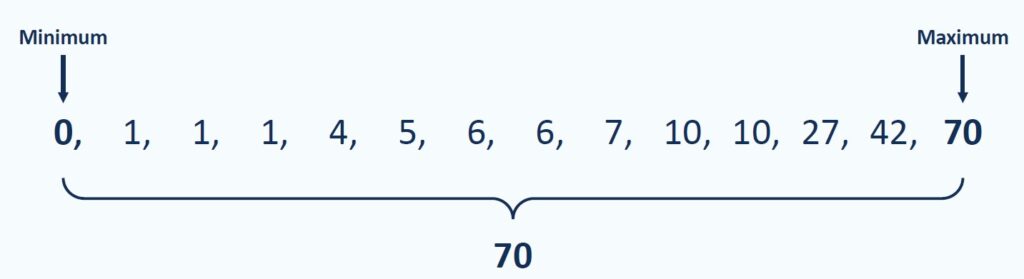
Considérons l’ensemble de données suivant : \(A = {0, 1, 1, 1, 4, 5, 6, 6, 7, 10, 10, 27, 42, 70}\).
- Le minimum de \(A\) est 0,
- Le maximum de \(A\) est 70,
- La plage de \(A\) est \(70 – 0 = 70\).
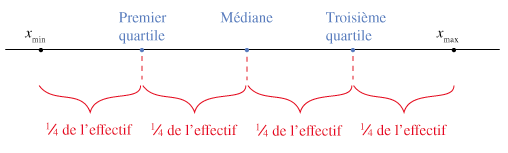
Les quartiles
Les quartiles sont des valeurs qui divisent un ensemble de données triées en quatre parties égales, appelées quartiers. Ils permettent d’obtenir une meilleure compréhension de la répartition des données et de la variabilité au sein de l’ensemble.
Il existe trois quartiles principaux, notés Q1, Q2 et Q3 :
- Premier quartile (Q1) : Il représente la 25ème percentile, ce qui signifie que 25% des valeurs dans l’ensemble de données lui sont inférieures ou égales.
- Deuxième quartile (Q2) : Il correspond à la médiane, qui représente la valeur centrale de l’ensemble de données une fois trié. Elle divise l’ensemble en deux parties égales : 50% des valeurs lui sont inférieures et 50% lui sont supérieures.
- Troisième quartile (Q3) : Il représente la 75ème percentile, ce qui signifie que 75% des valeurs dans l’ensemble de données lui sont inférieures ou égales.
La variance
Définition: La variance est une mesure statistique qui décrit l’étendue de la dispersion des valeurs d’un ensemble de données. Elle indique comment les valeurs de cet ensemble se répartissent autour de la moyenne. La variance mesure donc le degré de variation ou d’étalement des valeurs par rapport à la moyenne.
Formule:
\(\sigma^2 = \frac{\sum\limits_{i=1}^{n} (x_i – \overline{x})^2}{n – 1}\)
Où :
- \(\sigma^2\) est la variance
- \(\sum\limits_{i=1}^{n} (x_i – \overline{x})^2\) est la somme des carrés des écarts à la moyenne
- \({n}\) est le nombre d’observations
Étapes de calcul:
(a) Calcul de la moyenne:
La première étape consiste à calculer la moyenne de l’ensemble de données.
(b) Calcul des écarts à la moyenne:
Ensuite, on calcule l’écart entre chaque valeur et la moyenne.
(c) Calcul des carrés des écarts à la moyenne:
On calcule ensuite le carré de chaque écart à la moyenne.
(d) Somme des carrés des écarts à la moyenne:
On additionne ensuite tous les carrés des écarts à la moyenne.
(e) Division par le nombre d’observations moins 1:
On divise la somme obtenue par le nombre d’observations moins 1.
(f) Interprétation:
Exemple:
Considérons l’ensemble de données suivant :
\(A = {12, 15, 10, 14, 18}\)
(a) Calcul de la moyenne:
La moyenne de l’ensemble de données est de 13.8 (je ne suis pas magicien, on l’avait calculée précédemment 😊).
(b) Calcul des écarts à la moyenne:
\({12 – 13.8} = -1.8 \newline
{15 – 13.8} = 1.2 \newline
{10 – 13.8} = -3.8 \newline
{14 – 13.8} = 0.2 \newline
{18 – 13.8} = 4.2\)
(c) Calcul des carrés des écarts à la moyenne:
\((-1.8)^2 = 3.24 \newline
(1.2)^2 = 1.44 \newline
(-3.8)^2 = 14.44 \newline
(0.2)^2 = 0.04 \newline
(4.2)^2 = 17.64\)
(d) Somme des carrés des écarts à la moyenne:
\(3.24 + 1.44 + 14.44 + 0.04 + 17.64 = 36.8\)
(e) Division par le nombre d’observations moins 1:
\(\frac{36.8}{5 – 1} = 9.2\)
(f) Interprétation:
La variance de l’ensemble est de 9.2, cela indique le degré moyen de variation carrée des observations par rapport à la moyenne de l’ensemble des données. Plus précisément, cela signifie que, en moyenne, les carrés des écarts des valeurs par rapport à la moyenne de l’ensemble des données sont de 9.2.
L’écart type
Définition: L’écart type est une mesure de dispersion qui permet de quantifier la variabilité des valeurs d’un ensemble de données par rapport à la moyenne.
Formule:
La formule de l’écart type est la suivante :
\(\sigma = \sqrt{\frac{\sum\limits_{i=1}^{n} (x_i – \overline{x})^2}{n – 1}}\)
Où :
- \(\sigma\) est l’écart type
- \(\sum\limits_{i=1}^{n} (x_i – \overline{x})^2\) est la somme des carrés des écarts à la moyenne
- \({n}\) est le nombre d’observations
Étapes de calcul:
Les étapes de calcul de l’écart type sont les mêmes que celles de la variance. La seule différence est qu’à la fin, on calcule la racine carrée du résultat.
Considérons le même ensemble de données que précedemment :
\(A = {12, 15, 10, 14, 18}\)
(f) Racine carrée du résultat:
\(\sqrt{9.2} = 3.03\)
(g) Interprétation:
L’écart type de l’ensemble de données est de 3.03. Cela signifie que les valeurs de l’ensemble de données sont dispersées autour de la moyenne de 3.03, avec une moyenne de 3.03 unités d’écart.
La forme des distributions
L’autre aspect aussi important dans les statistiques descriptives est la forme des distributions statistiques peut être décrite à l’aide de deux concepts clés : l’asymétrie (skewness) et l’aplatissement (kurtosis). Ces mesures fournissent des informations importantes sur la forme et les caractéristiques d’une distribution de données.
Asymétrie (Skewness)
L’asymétrie mesure le degré de distorsion ou d’inclinaison d’une distribution par rapport à une distribution normale. Elle indique si les données s’étalent plus d’un côté de la moyenne que de l’autre.
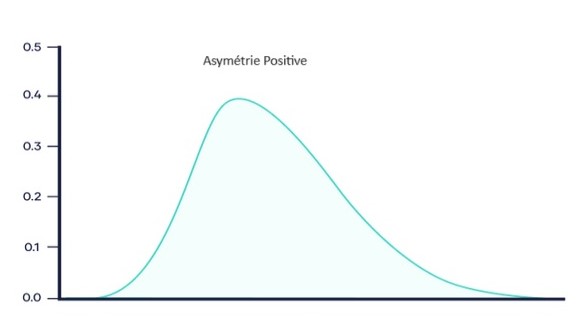
Asymétrie positive (skewness positif) : Si la queue de la distribution s’étend plus loin vers les valeurs positives (à droite de la moyenne), la distribution est dite asymétrique positive. Cela signifie qu’il y a une concentration de données vers les valeurs inférieures, avec une queue s’étendant vers les valeurs supérieures.
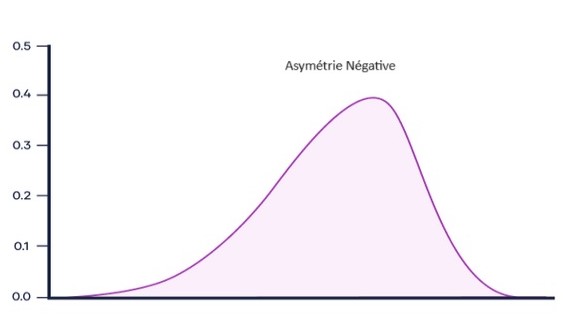
Asymétrie négative (skewness négatif) : Si la queue de la distribution s’étend plus vers les valeurs négatives (à gauche de la moyenne), la distribution est asymétrique négative. Cela indique une concentration de données vers les valeurs supérieures, avec une queue s’étendant vers les valeurs inférieures.
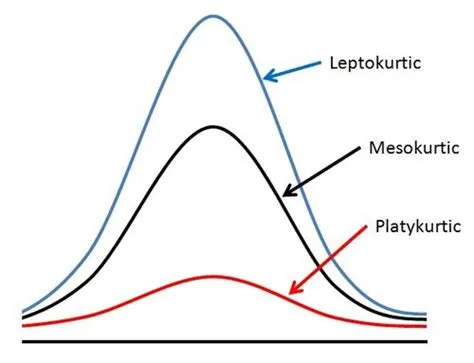
Aplatissement (Kurtosis)
L’aplatissement mesure le degré de pointe ou d’aplatissement d’une distribution par rapport à une distribution normale. Il décrit la concentration des données autour de la moyenne.
- Kurtosis élevé (Leptokurtic) : Une valeur de kurtosis supérieure à celle de la distribution normale indique une distribution plus pointue, avec des queues plus épaisses. Cela signifie que les données sont plus concentrées autour de la moyenne, avec plus d’observations extrêmes (outliers) que dans une distribution normale.
- Kurtosis faible (Platykurtic) : Une valeur de kurtosis inférieure à celle de la distribution normale indique une distribution plus aplatie, avec des queues plus fines. Cela suggère une dispersion plus large des données autour de la moyenne, avec moins d’observations extrêmes par rapport à une distribution normale.
- Kurtosis de la distribution normale (Mesokurtic) : Une distribution avec un kurtosis similaire à celui de la distribution normale est qualifiée de mesokurtique. Elle présente un équilibre entre la pointe de la distribution et la dispersion des queues.
Maintenant c’est quoi les statistiques inférentielles ?
Contrairement aux statistiques descriptives, les statistiques inférentielles vont plus loin que la simple description. Elles permettent de tirer des conclusions sur une population entière à partir d’un échantillon.
Échantillonnage et population
Imaginez que vous voulez savoir la taille moyenne des habitants d’une ville. Il est impossible de mesurer tout le monde ! On se base donc sur un échantillon, un groupe d’individus représentatif de la population (par exemple, 100 habitants choisis aléatoirement).
Tests statistiques (tests d’hypothèse)
Les statistiques inférentielles utilisent des tests d’hypothèse pour vérifier des affirmations sur la population à partir des données de l’échantillon. Par exemple, on pourrait tester l’hypothèse selon laquelle la taille moyenne des habitants de la ville A est supérieure à celle de la ville B.
Exemple
Imaginons que nous voulons tester si la durée moyenne de vie d’une marque de piles est bien de 36 mois, comme le prétend le fabricant. Nous avons un échantillon de 25 piles de cette marque, et après les avoir testées, nous trouvons que la durée de vie moyenne dans notre échantillon est de 34 mois, avec un écart-type de 5 mois. Nous allons utiliser un niveau de confiance de 95%.
Voici les étapes que nous devons suivre:
- Énoncer l’hypothèse nulle (\(H_0\)) et l’hypothèse alternative (\(H_1\))
- Choisir l’intervale de confiance
- Selectionner le test statistique à faire
- Appliquer le test et calculer la p-valeur
- Tirer une conclusion à propos de l’hypothèse nulle (\(H_0\))
Énoncer l’hypothèse nulle et l’hypothèse alternative
- Hypothèse nulle (\(H_0\)): La durée de vie moyenne des piles est de 36 mois. \(\mu=36\)
- Hypothèse alternative (\(H_1\)): La durée de vie moyenne des piles n’est pas de 36 mois. \(\mu \neq 36\)
Choisir l’intervale de confiance
Nous travaillons avec un intervalle de confiance de 95% (\(\alpha = 0.05\)). \(\alpha\) est connu sous le nom de seuil de signification ou niveau de signification. Il représente la probabilité de rejeter à tort une hypothèse nulle vraie (erreur de type I). En termes plus simples, il représente le risque de commettre une erreur en concluant qu’il existe une différence significative alors qu’il n’en existe en réalité pas.
Sélectionner le test statistique à faire
Puisque la taille de l’échantillon est inférieure à 30, nous allons utiliser le test t de Student pour un échantillon. Le test t est approprié ici car nous ne connaissons pas l’écart-type de la population.
Appliquer le test et calculer la p-valeur
La formule du test t pour un échantillon est:
\(t = \frac{\bar{x} – \mu_0}{\frac{s}{\sqrt{n}}}\)
Où:
- \(t\) est la significativité, elle évalue la significativité des différences dans les données d’échantillon,
- \(\bar{x}\) est la moyenne de l’échantillon,
- \(\mu_0\) est la moyenne de la population sous \(H_0\),
- \({s}\) est l’écart type de l’échantillon,
- \({n}\) est la taille de l’échantillon.
En substituant les valeurs connues:
\(t = \frac{\bar{x} – \mu_0}{\frac{s}{\sqrt{n}}} = \frac{34 – 36}{\frac{5}{\sqrt{25}}} = -2.0\)
Détermination des degrés de liberté
Les degrés de liberté pour ce test sont \({n – 1} = 25−1= 24\)
Calcul de la p-valeur
La p-valeur est calculée en utilisant la fonction de répartition cumulative (CDF) de la distribution t de Student. Puisque c’est un test bilatéral, nous multiplions le résultat par 2 pour obtenir la p-valeur pour les deux extrémités de la distribution.
Le choix entre un test bilatéral (ou à deux queues) et unilatéral (ou à une queue) dans le cadre d’un test t de Student dépend de la nature de l’hypothèse alternative que vous souhaitez tester. Voici une explication claire de quand utiliser chacun :
Test Unilatéral (à une queue)
Un test unilatéral est utilisé lorsque l’hypothèse alternative spécifie une direction dans laquelle les valeurs peuvent différer de l’hypothèse nulle. Autrement dit, vous utilisez un test unilatéral si vous avez une raison de croire que la différence sera soit strictement positive, soit strictement négative. Il y a deux types de tests unilatéraux :
- Test à une queue à droite : Vous utilisez ce test si vous pensez que la moyenne de l’échantillon sera supérieure à la moyenne de la population sous l’hypothèse nulle. L’hypothèse alternative est donc formulée comme \(\mu \gt \mu_0\).
- Test à une queue à gauche : Ce test est approprié si vous pensez que la moyenne de l’échantillon sera inférieure à la moyenne de la population sous l’hypothèse nulle. L’hypothèse alternative est \(\mu \lt \mu_0\).
Test Bilatéral (à deux queues)
Un test bilatéral est utilisé quand vous voulez tester si la moyenne de l’échantillon est significativement différente de la moyenne de la population sous l’hypothèse nulle, sans spécifier la direction de la différence. Cela signifie que vous cherchez à savoir si la moyenne de l’échantillon est soit significativement plus grande, soit significativement plus petite que la moyenne de la population. L’hypothèse alternative est formulée comme \(\mu \neq \mu_0\).
Revenons au calcul de p-valeur
J’ai utilisé Scipy qui est une bibliothèque Python de Machine Learning et Numpy qui est une bibliothèque pour langage de programmation Python, destinée à manipuler des matrices ou tableaux multidimensionnels. J’aurai aussi pu faire les calculs des statistiques descriptives avec Python, mais ça sera l’objet d’un autre article.
# statistiques descriptives et inférentielles from scipy.stats import t import numpy as np # Valeurs données n = 25 # taille de l'échantillon x_bar = 34 # moyenne de l'échantillon mu_0 = 36 # moyenne sous H0 s = 5 # écart-type de l'échantillon alpha = 0.05 # seuil de significativité # Calcul de la statistique de test t t_stat = (x_bar - mu_0) / (s / np.sqrt(n)) # Degrés de liberté df = n - 1 # Calcul de la p-valeur p_value = 2 * t.cdf(t_stat, df) # Multiplié par 2 pour le test bilatéral t_stat, p_value
Les résulats sont les suivants:
(-2.0, 0.056939849936591666)
Avec une p-valeur de 0.05690.0569, qui est supérieure au seuil de signification de 0.05, nous ne pouvons pas rejeter l’hypothèse nulle à un niveau de confiance de 95%. Cela signifie qu’il n’y a pas suffisamment de preuves pour affirmer que la durée de vie moyenne des piles est différente de 36 mois.
Conclusion
En conclusion, les statistiques descriptives et inférentielles constituent les deux piliers fondamentaux sur lesquels repose l’analyse de données dans l’ère du Big Data. Les statistiques descriptives vous équipent des outils nécessaires pour résumer et comprendre les grandes lignes de vos données, en offrant une vue d’ensemble à travers les mesures de tendance centrale, de dispersion et la forme des distributions. D’autre part, les statistiques inférentielles ouvrent la porte à la généralisation de vos observations à des populations plus larges, en permettant de tester des hypothèses, de calculer des p-valeurs et de prendre des décisions éclairées basées sur des intervalles de confiance prédéfinis.
Cet article a exploré comment, en maîtrisant ces deux approches, vous pouvez non seulement décrire ce qui est observé dans votre ensemble de données mais aussi prédire et expliquer des phénomènes qui ne sont pas immédiatement apparents. Pour les professionnels et les aspirants du monde de la donnée, cette compréhension est cruciale pour transformer des données brutes en insights actionnables, soutenant ainsi la prise de décision stratégique dans les organisations.
Questions fréquentes sur les statistiques descriptives et inférentielles
FAQ
- Laquelle des deux statistiques est la meilleure ?
Il n’y a pas de “meilleure” méthode, tout dépend de votre objectif. La statistique descriptive est utile pour résumer des données, tandis que la statistique inférentielle est utile pour tirer des conclusions.
- Est-ce que la statistique est difficile à apprendre ?
Il existe des notions de base en statistique qui sont relativement simples à comprendre. Cependant, la statistique peut devenir plus complexe si vous souhaitez utiliser des méthodes avancées.
- Y a-t-il des logiciels pour faire de la statistique ?
Oui, il existe de nombreux logiciels de statistique, comme Excel, R et SPSS et même Python.
- Quelle est la différence entre la variance et l'écart type ?
La variance et l’écart type sont deux mesures statistiques qui servent à quantifier la dispersion ou la variabilité des données dans un ensemble. Bien qu’ils soient étroitement liés, ils ne mesurent pas la dispersion de la même manière et sont utilisés dans différents contextes pour fournir des informations sur la distribution des données.
Variance : La variance mesure la dispersion des données par rapport à leur moyenne. Elle est calculée comme la moyenne des carrés des écarts entre chaque valeur de l’ensemble de données et la moyenne de cet ensemble. En termes simples, elle répond à la question : “À quel point les différentes valeurs de cet ensemble s’écartent-elles de la moyenne ?” La variance est exprimée en unités au carré, ce qui peut rendre son interprétation moins intuitive.
Écart type : L’écart type est la racine carrée de la variance. Il mesure également la dispersion des données, mais étant donné qu’il est exprimé dans les mêmes unités que les données elles-mêmes, il est souvent plus facile à comprendre et à interpréter que la variance. L’écart type indique en moyenne à quel point les valeurs individuelles diffèrent de la moyenne de l’ensemble.